در خیلی از مسائل آمار و احتمال ما باید تمام حالت های ممکن برای شرایط داده شده رو فهرست کنیم یا حداقل اونا رو بشمریم.
بیاید این مقاله رو با مثالی ابتدایی شروع کنم:
Suppose that someone wants to go by plane on a week’s vacation to one of the five cities; New York, Washington, Los Angles, San Francisco, Chicago.
برای استفاده در قسمتای بعد تعداد راه ها رو با نمودار درختی نشون میدم:
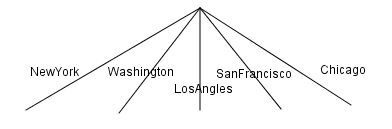
واضحه که فقط 5 انتخاب برای مسافرت وجود داره. حالا بیاید تعداد روش های سفرشو بیشتر کنیم:
Suppose that someone wants to go by bus, train, or plane on a week’s vacation to one of the five cities, New York, Washington, Los Angles, San Francisco, Chicago. Find the number of different ways in which this can be done.
اگه بازم نمودار بکشیم داریم:
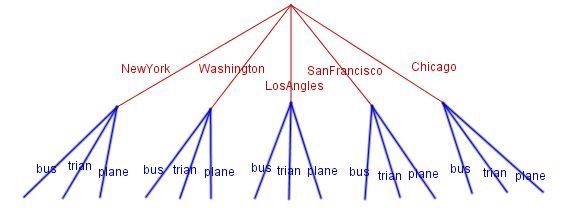
حالا با اضافه شدن وسایل نقلیه دیگه 15 انتخاب وجود داره. اول انتخاب شهر و سپس انتخاب وسیله نقلیه.
برای شمارش حالات ما اغلب از قضیه زیر استفاده می کنیم:
قضیه اساسی شمارش: اگر عملی شامل دو مرحله باشه که مرحله اول به n1 راه انجام بشه و برای هر یک از این راه ها، مرحله دوم بتونه به n2 راه صورت بگیره آنگاه کل عمل میتونه به n1n2 روش انجام بشه.
در مثال قبل مرحله اول یعنی تعداد شهرها 5 تا بود و مرحله دوم یعنی انتخاب وسیله نقلیه 3 تا بود پس در کل 15 روش برای مسافرت وجود داشت.
قضیه بعدی درواقع تعمیمی از قضیه قبله:
اگر عملی شامل k مرحله باشه که مرحله اول به n1 راه انجام بشه و و برای هر یک از این راه ها، مرحله دوم بتونه به n2 راه صورت بگیره و برای هر یک از راه های دو مرحله نخستین، مرحله سوم بتونه به n3 راه انجام بگیره و الی آخر اونوقت کل عمل میتونه به n1n2...nk راه انجام بشه.
A quality control inspector wishes to select a part for inspection from each of four different bins containing 4, 3, 5, and 4 parts, respectively. In how many different ways can she choose the four parts?
با توجه به قضیه قبل تعداد کل راه های انتخاب برابره با 4×3×5×4=240 .
In how many different ways can one answer all the questions of a true–false test consisting of 20 questions?
روی هم رفته تعداد روش متفاوت برای جواب دادن به همه 20 سوال وجود داره. که فقط یه حالت وجود داره که کسی به همه سوالات صحیح جواب بده و فقط یه حالت وجود داره که کسی به همه سوالات غلط جواب بده.
A student can study 0, 1, 2, or 3 hours for a history test on any given day. How many ways are there in which the student can study at most 4 hours for the rest on two consecutive days?
اگه دقت کنید میبینید که این سوال با قبلیا فرق داره. در واقع یه قید یا محدودیت توی سوال مطرح شده و به همین خاطر تعداد راه های مرحله دوم کاملا به مرحله اول بستگی داره. مثلا دانش آموز نمیتونه روز اول 2 ساعت و روز دوم 3 ساعت درس بخونه. بنابراین باید با دقت بیشتری عمل کرد. بذارید از نمودار درختی استفاده کنیم:
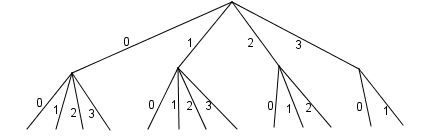
اگه تعداد راه ها (شاخه ها) رو بشمریم میبینیم که دانش آموز به 13 روش میتونه جوری درس بخونه که در طول دو روز بیشتر از 4 ساعت درس نخونه