چند مثال از کفایت داده ها حالا که چهار روش حل مسائل کفایت داده ها در GMAT را یاد گرفتیم بیایید چند مسئله با هم حل کنیم.

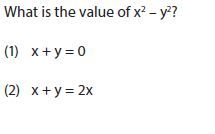
این سوال را باید با استفاده از تکنیک های جبری حل کرد.

همینطور که میبینید در صورت سوال یک اتحاد مزدوج (difference of squares) وجود دارد. ( مسلما شما باید اتحادهای مهم را یاد بگیرید). با دیدن اتحاد مزدوج x2-y2 شما باید سریعا دو سوال را در نظر بگیرید:

اول اینکه مقدار x2-y2 چیست و دوم اینکه مقدار (x+y)(x-y) چیست؟

گزاره 1 مسلما کافیست، چون مقدار سوال دوم را صفر میکند.

از گزاره دوم داریم:

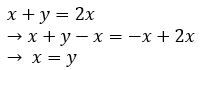
بنابراین x-y=0 و درنتیجه بازهم جواب صفر است. پس این گزاره هم کافیست.بنابراین جواب سوال گزینه D است(چون هر دو گزینه به تنهایی کافی هستند)

همانطورکه قبلا هم گفتم اغلب مردم تمایل دارند در GMAT  تنها گزاره ها را دستکاری کنند و سوال اصلی را رها میکنند. دیدید که در این سوال دستکاری جبری سوال اصلی چقدر راهگشا بود و البته گزاره ها را هم دستکاری کردیم.اما اشتباه مهلکی که اکثر مردم مرتکب میشوند این است که با تایید کافی بودن گزاره 1 تمرکز لازم روی سوال را از دست داده و حتی گاهی به گزاره دوم نگاه هم نمیکنند.

بریم سراغ سوال بعدی GMAT :

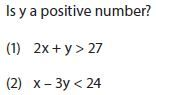
در اینگونه سوال ها شما باید مفهوم بخشپذیری را به خوبی فرا گرفته باشید. دستکاری جبری در این سوال کمکی نخواهد کرد.

عدد بسیار یزرگ است پس مسلما انتخاب اعداد و همینطور محاسبه تنها هم کمکی نخواهند کزد چون محاسبه عدد ناممکن است.

هدف هر گزاراه اینست که آیا k عددی اول است یا خیر. اگر شما بتوانید ثابت کنید که k بر عددی غیر از 1 و خودش بخشپذیر است آنگاه k اول نیست.

در اینطور سوالات شما باید به دنبال اثبات نقیض سوال بروید و جواب خیر را بیابید.

در گزاره 1 میبینیم که به جای m میتوانیم هر یک از اعداد 2 یا 3 یا 4 یا 5 یا 6 یا 7 را قرار دهیم، از طرف دیگر میدانیم که 1×2×3×4×5×6×7×8×9×10=!10 پس اگر !10 با هر یک از اعداد فوق جمع شود حتما بر آن عدد بخشپذیر است. مثلا 7+!10 حتما بر 7 بخشپذیر است. بنابراین گزاره 1 جواب خیر را نتیجه میدهد پس گزاره 1 کافیست.

در گزاره 2 باید کمی احتیاط کنیم. اشتباه خیلی از مردم اینست که هنگام بررسی گزاره 2 هنوز گزاره 1 راهم در ذهن دارند. گزاره 1 را فراموش کنید. یعنی ممکن است گزاره 2 را با این فرض اضافی بررسی کنند که k بزرگتر از !10 است.

شاید فکر کنیدکه گزاره 2 کافیست چون هر مضربی از 7 حتما بر 7 بخشپذیر است اما دقت کنید که خود 7 هم مضربی از 7 است اما عددی اول نیز هست. پس گزاره 2 ناکافیست.

بنابراین جواب صحیح گزاره A است.

اما سوال بعدی GMAT :

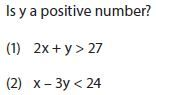
 خیلی از سوالات مربوط به نامساویها مخصوصا سوالات مربوط به مثبت یا منفی بودن با استفاده از مفاهیم قابل حل هستند اما گاهی هم مثل این مسئله استفاده از مفاهیم مسئله را پیچیده تر میکند. هر وقت که در شک بودید، بهترین راه حل اینست که صرفا شروع کنید و سعی کنید مسئله را با محاسبات ریاضی حل کنید.

از صورت گزاره ها به راحتی میتوان فهمید که هیچیک از گزاره ها به تنهایی کافی نیستند و x هر مقداری میتواند داشته باشد. پس باید با هم در نظر گرفته شوند و این یعنی این که دست شما برای انجام عملیات ریاضی باز است چون با یک دستگاه دو نامعادله و دو مجهول روبرو هستید که مسلما قابل حل است.

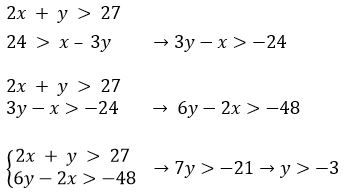
ابتدا نامساوی دوم را در 1- ضرب میکنیم:

حالا نامساوی دوم را در 2 ضرب میکنیم:

حالا دو نامساوی را جمع میکنیم:

پس y هر مقدار بزرگتر از 3- را میتواند داشته باشد.

فرض کنیم y مقدار 31 داشته باشد آنگاه برای درست بودن نامساوی اول x باید مقداری منفی بگیرد و اگر y صفر باشد آنگاه x مثبت خواهد بود. پس هر دو گزاره ناکافی هستند.

جواب صحیح گزینه E است.

و سوال آخرGMAT :

If x is a positive integer less than 30, is x odd?

(1) When x is divided by 3, the remainder is 2.

(2) When x is divided by 5, the remainder is 2.

در حالیکه این سوال DATA SUFFICIENY را میتوان به صورت مفهومی حل کرد اما راه ساده تر استفاده از روش انتخاب اعداد است. یادمان باشد که همیشه باید اعدادی را انتخاب کنیم جواب رد به مابدهند.

صورت سوال از ما میخواهد که فرد بودن x را مشخص کنیم پس بیایید در گزاره 1 یک عدد فرد انتخاب کنیم و البته کوچکتر از 30.

5 عددی است که در گزاره 1 صدق میکند یعنی باقیمانده آن با تقسیم بر 3 عدد 2 است. پس x میتواند فرد باشد.

حالا که جواب سوال بله شد باید عدد را عوض کنیم و به دنبال یافتن جواب خیر باشیم. باید عددی زوج بیابیم که در گزاره 1 صدق کند. با کمی تحقیق عدد 8 را میابیم. پس گزاره 1 کافی نیست.

 برای گزاره 2 هم اعداد 7 و 12 صادق هستند پس این گزاره هم ناکافیست.

 در این مرحله باید دو گزاره را با هم در نظر بگیریم یعنی باید عددی بیابیم که با تقسیم بر 3 و هم با تقسیم بر 5 باقیمانده 2 داشته باشد. اینجا میتوان همه اعدادی که باقسیم بر 3 باقیمانده 2 دارند را به ترتیب بنویسیم و همینکار را نیز برای 5 تکرار کنیم وعدد مشترک را یافته و جواب سوال را بدهیم. اگر اینکار را انجام دهیم به عدد 17 میرسیم اما مسلما اینکار زمانبر است.

اگر کمی نظریه اعداد بدانیم میبینیم که  عددی که با تقسیم بر 3 و 5 یک باقیمانده دارد با تقسیم بر حاصلضرب آنها یعنی 15 هم باید همان باقیمانده را داشته باشد و تنها عدد کوچکتر از 30 که این شرایط را دارد عدد 17 است که عددی فرد است.

اما بازی هنوز تمام نشده است یک عدد را یادمان رفت.

همه ما در تقسیم همیشه اعدادی را به عنوان مقسوم (dividend) انتخاب میکنیم که بزرگتر از مقسوم علیه (divisor) هستند اما مقسوم میتواند کوچکتر هم باشد. مثلا در این سوال میتوانستیم از همان ابتدا عدد 2 را انتخاب کنیم که عددی زوج است و با تقسیم بر 3 و 5 همیشه باقیمانده 2 میشود. 

بنابراین جواب گزینه E است.

حتما متوجه شده اید که انتخاب عدد واقعا کار سختی است و گاهی ناکارآمد ولی همیشه بهترین راه برای رد گزینه ها یا گزاره ها است.