سوالات کفایت داده بر دو نوع هستند:

-          بله یا خیر (yes or no)

-          چقدر است؟ (what is the value?)

برای سوالات بله یا خیر دو نوع تله رایج وجود دارد.

1.    گزاره ای که چندین مقدار در اختیار شما میگذارد اما تمام مقدارها پاسخ یکسانی به سوال بله یا خیر می دهند.

2.    گزاره ای که تنها جواب خیر در بر دارد – اما چون خیر نیز یک جواب کامل است پس گزاره کافیست- دقت کنید که هدف ما این نیست که ثابت کنیم جواب بله است.

بگذارید با چند تمرین منظورم را واضحتر بیان کنم

   واضح است که گزاره دو جواب 4 و 4- را نتیجه میدهد که بزرگتر از 5 نیستند بنابراین پاسخ مسئله خیر است که کافیست. یعنی گزاره کافیست.

Is  greater than 5?  

 با یک معادله خطی روبرو هستیم که طبیعتا یک جواب منحصر به فرد دارد. بنابراین گزاره کافی خواهی بود. ( دقت کنید که نیازی به حل کردن معادله نیست)

برای سوالات 'چقدر است؟' بیشتر اشتباهات آزمون دهندگان، فرضیات ناصحیحی است که در مورد مسئله یا قیود آن میکنند. در این گونه سوالات اشتباهات زیر رایج هستند:

1.    آزمون دهندگان اعداد را صحیح یا مثبت در نظر میگیرند. با این مفروضات گزاره به نظر کافی میرسد در حالی که اعداد دیگری نیز وجود دارند.

2.    آزمون دهندگان قیدهایی را که در آن نوع اعداد (برای مثال اعداد صحیح) بیان شده است را نادیده میگیرند و بنابراین فکر میکنند چندین امکان برای مسئله وجود دارد در حالی که دقیقا یک مقدار دارد.

دو مثال زیر را درنظر بگیرید:

What is the value of x?

در این مسئله در نگاه اول به نظر آسان میرسد که مقدار x را 9 در نظر بگیریم. در حالیکه اگر 9x را به سمت چپ ببریم آنگاه داریم:

  درنتیجه x میتواند مقدار 0 نیز داشته باشد. پس گزاره کافی نیست.

 What is the value of x?

در مسئله قبل باید به یاد داشته باشیم که اغلب معادلات درجه 2 دارای دو جواب هستند (در واقع حداکثر دارای دو جواب حقیقی هستند). بنابراین شاید فکر کنید که گزاره دارای دو جواب است و در نتیجه کافی نیست. اما داریم:

  پس x برابر است با 12. یعنی گزاره کافیست.

حالا بیاید برای تمرین بیشتر چند مسئله واقعی GMAT حل کنیم:

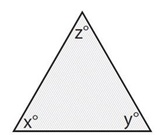
Is the triangle above equilateral?

(1) x = y

(2) z = 50

گزینه 1 این نتیجه را میدهد که مثلث بالا متساوی الساقین است و شاید متساوی الاضلاع باشد، پس این گزاره کافی نیست.

اما گزاره 2 میگوید که مثلث متساوی الاضلاع نیست چون یک زاویه 50 درجه دارد. در صورتیکه زاویه های یک مثلث متساوی الاضلاع با هم برابر و 60 درجه هستند. پس جواب مسئله خیر است و بنابراین گزاره 2 کافیست.

دقت کنید که در اینگونه سوالات ذهن ما با رسیدن به جواب خیر سریعا گزاره 2 را حذف میکند و چون گزاره 1 هم کافی نیست در نهایت گزینه E را انتخاب میکند.

دقت در کلمات در این سوالات بسیار مهم هستند. مثلا در مسئله بالا اگر کلمه متساوی الاضلاع (equilateral) با کلمه متساوی الساقین (Isosceles) عوض شود آنگاه گزاره 1 تبدیل به کافی و گزاره 2 ناکافی خواهد شد.

What is the value of x?

 گزاره 1 میخواهد شما فکر کنید که x یک عدد صحیح است. چون خواهیم دید که

 در واقع حتی میخواهد شما فکر کنید که x=4.

گزاره 2 میخواهد شما فکر کنید که x یک عدد مثبت است و با یادآوری گزاره 1 یک عدد صحیح مثبت است.

اگر شما از گزاره 1 استفاده کنید باید x را یک عدد صحیح مثبت بزرگتر از 3 فرض کنید، پس x=4.

اما باید توجه کنیم که سوال اصلی چیزی راجع به نوع عدد نمیگوید پس x یک عدد حقیقی میتواند باشد. پس گزاره 1 کافی نیست.

گزاره 2 هم کافی نیست چون دو مقدار 4 و -4 را نتیجه میدهد. پس باید گزینه C را در نظر بگیریم. ترکیب گزاره 1 و 2 با هم نتیجه میدهد که x=4. پس ترکیب دو گزاره کافیست و جواب گزینه C است.